1. 문제 정보
- https://www.acmicpc.net/problem/1109
- Platinum IV
- 그래프
2. 문제 풀이
문제를 처음 봤을 때, 트리의 높이 문제라고 생각은 했으나 어떻게 트리를 구현해야 할 지 감이 잘 오지 않았어요 🥲
트리로 구현하려고 할 때 처음부터 한 번에 트리로 구현하려고 하니 많이 막혔던 것 같아요
트리로 구현하지 않아도 풀 수 있는 방법도 있었구요 ! (지인이 이렇게 풀었더라구요 👀)
각각의 풀이 방법을 설명드릴게요
- 트리 구현 풀이법 (BFS 3회, DFS 1회)
트리를 직접 구현해서 푸는 방식입니다
# https://www.acmicpc.net/board/view/85099 13 17 xxxxxxxxxxxxxxxxx x...............x x.xxx.x...xxxxx.x x.xxxx....x...x.x x.........x.x.x.x x...xxxxx.x...x.x x...x...x.xxx.x.x x...x.x.x...x...x x...x...x...xxx.x x....xxxxxx.....x x.x.............x x...............x xxxxxxxxxxxxxxxxx
첫 번째 BFS에서 각 섬에 라벨링을 진행해요
11111111111111111 1...............1 1.222.2...33333.1 1.2222....3...3.1 1.........3.4.3.1 1...55555.3...3.1 1...5...5.333.3.1 1...5.6.5...3...1 1...5...5...333.1 1....555555.....1 1.7.............1 1...............1 11111111111111111
그다음, 두 번째 BFS를 진행해 인접 리스트를 만듭니다
이때 루트가 될 섬(가장 외부에 위치한 섬)도 같이 지정합니다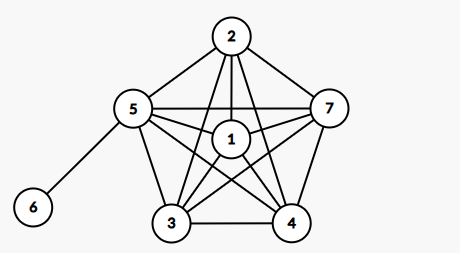
그럼 이와 같은 그래프가 완성됩니다
여기서 세 번째 BFS를 진행하는데, 이때 루트(1번 정점)를 통해 BFS를 진행해주면
이와 같은 상태가 돼요 !
즉, 탐색 순서에 따라 그래프를 저장한다면 이와 같이 트리 형태로 나타낼 수 있게 됩니다 😊
마지막 DFS는 후위 순회 방식을 이용해 각 섬의 높이가 얼마인지 구하고, 구해진 섬의 높이의 갯수를 저장합니다
이에 대한 코드는 아래와 같습니다
#include <iostream> #include <vector> #include <queue> #include <set> using namespace std; int n, m; char x; int MAP[50][50]; bool visit[50][50]; bool* visit_island; int ans[50]; int NUM = 1; int max_height = 0; int dx[8] = { -1, 1, 0, 0, -1, -1, 1, 1 }; int dy[8] = { 0, 0, -1, 1, -1, 1, -1, 1 }; vector<set<int>> graph; vector<vector<int>> tree; set<int> roots; void labeling(int ix, int iy, int num) { queue<pair<int, int>> q; q.push({ ix, iy }); visit[ix][iy] = true; MAP[ix][iy] = num; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (int i = 0; i < 8; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue; if (!visit[nx][ny] && MAP[nx][ny] == -1) { visit[nx][ny] = true; MAP[nx][ny] = num; q.push({ nx, ny }); } } } } void make_graph(int ix, int iy, int num) { queue<pair<int, int>> q; q.push({ ix, iy }); visit[ix][iy] = true; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= n || ny >= m) { roots.insert(num); } else if (!visit[nx][ny]) { if (MAP[nx][ny] == 0 || MAP[nx][ny] == num) { visit[nx][ny] = true; q.push({ nx, ny }); } else { graph[num].insert(MAP[nx][ny]); graph[MAP[nx][ny]].insert(num); } } } } } void make_tree(int num) { queue<int> q; q.push(num); visit_island[num] = true; while (!q.empty()) { int x = q.front(); q.pop(); for (int adj : graph[x]) { if (!visit_island[adj] && roots.find(adj) == roots.end()) { visit_island[adj] = true; tree[x].push_back(adj); q.push(adj); } } } } int post_order(int num) { int height = 0; for (int adj : tree[num]) { height = max(height, post_order(adj) + 1); } max_height = max(max_height, height); ans[height]++; return height; } int main() { ios_base::sync_with_stdio(0); cin.tie(0); cin >> n >> m; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { cin >> x; if (x == 'x') { MAP[i][j] = -1; } else if (x == '.') { MAP[i][j] == 0; } } } for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (MAP[i][j] == -1) { labeling(i, j, NUM); NUM++; } } } if (NUM == 1) { cout << -1; return 0; } visit_island = new bool[NUM] {false}; graph.resize(NUM); tree.resize(NUM); for (int k = 1; k < NUM; k++) { fill_n(visit[0], 2500, false); for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (MAP[i][j] == k) { make_graph(i, j, k); } } } } for (int i = 1; i < NUM; i++) { if (roots.find(i) == roots.end()) continue; make_tree(i); } for (int i = 1; i < NUM; i++) { if (roots.find(i) == roots.end()) continue; post_order(i); } for (int i = 0; i <= max_height; i++) { cout << ans[i] << " "; } }
- 그래프 풀이법 (BFS 2회, DFS 1회)
그래프로 풀이하는 방법은 여기서 트리를 만드는 과정을 제거하는 대신 트리처럼 DFS 탐색을 진행시키는 방법이에요 !
이때는 부모(Parent)와 형제(Sibling)을 구분하는 방법으로 풀이해요
루트를 미리 정해뒀기 때문에 루트로부터 순회를 돌면 되고, 이때 부모값을 같이 파라미터로 보내줍니다
그리고 부모가 현재 정점과 연결된 정점과 연결되어 있으면 이는 사이클이 형성되어 있는 것이죠
사이클을 형성하고 있는 이 정점은 Sibling임을 이용해서 푸는 방식입니다
앞서 봤던 이 사진에서 3번 정점과 5번 정점은 연결되어있지만, 부모-자식 관계로 연결된 것이 아닌 형제로 연결되었죠?
이렇듯 이 부분을 통해 계산하는거에요 ! 😀
예를 들어, 5번 정점의 관계를 조사하려고 하고, 5번 정점이 DFS를 통해 1번으로부터 탐색해왔다고 합시다 (Parent = 1)
이때 Parent의 인접 리스트에 2번과 3번이 같이 존재하므로 이는 Sibling으로 판단
5번의 인접 리스트 중 Sibling과 Parent에 속하지 않은 정점은 6번만 남게 됩니다
그러므로 트리의 순회에 맞춰 다음 순회 장소로 선택할 정점은 6이 됩니다 🤗
#include <iostream> #include <vector> #include <queue> #include <set> using namespace std; int n, m; char x; int MAP[50][50]; bool visit[50][50]; bool* visit_island; int ans[50]; int NUM = 1; int max_height = 0; int dx[8] = { -1, 1, 0, 0, -1, -1, 1, 1 }; int dy[8] = { 0, 0, -1, 1, -1, 1, -1, 1 }; vector<set<int>> graph; set<int> roots; void labeling(int ix, int iy, int num) { queue<pair<int, int>> q; q.push({ ix, iy }); visit[ix][iy] = true; MAP[ix][iy] = num; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (int i = 0; i < 8; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue; if (!visit[nx][ny] && MAP[nx][ny] == -1) { visit[nx][ny] = true; MAP[nx][ny] = num; q.push({ nx, ny }); } } } } void make_graph(int ix, int iy, int num) { queue<pair<int, int>> q; q.push({ ix, iy }); visit[ix][iy] = true; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if (nx < 0 || ny < 0 || nx >= n || ny >= m) { roots.insert(num); } else if (!visit[nx][ny]) { if (MAP[nx][ny] == 0 || MAP[nx][ny] == num) { visit[nx][ny] = true; q.push({ nx, ny }); } else { graph[num].insert(MAP[nx][ny]); graph[MAP[nx][ny]].insert(num); } } } } } int post_order(int num, int parent) { int height = 0; visit_island[num] = true; for (int adj : graph[num]) { if (visit_island[adj] || roots.find(adj) != roots.end() || (parent != -1 && graph[parent].find(adj) != graph[parent].end())) continue; height = max(height, post_order(adj, num) + 1); } max_height = max(max_height, height); ans[height]++; return height; } int main() { ios_base::sync_with_stdio(0); cin.tie(0); cin >> n >> m; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { cin >> x; if (x == 'x') { MAP[i][j] = -1; } else if (x == '.') { MAP[i][j] == 0; } } } for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (MAP[i][j] == -1) { labeling(i, j, NUM); NUM++; } } } if (NUM == 1) { cout << -1; return 0; } visit_island = new bool[NUM] {false}; graph.resize(NUM); for (int k = 1; k < NUM; k++) { fill_n(visit[0], 2500, false); for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (MAP[i][j] == k) { make_graph(i, j, k); } } } } for (int i = 1; i < NUM; i++) { if (roots.find(i) == roots.end()) continue; post_order(i, -1); } for (int i = 0; i <= max_height; i++) { cout << ans[i] << " "; } }
이쪽 풀이가 과정도 더 짧고, 효율성도 더 좋게 나오네요 😊
'코딩테스트 > BAEKJOON' 카테고리의 다른 글
| 백준: 1106. 호텔 (C++) (0) | 2025.03.07 |
|---|---|
| 백준: 15708. 미네크래프트 (C++) (0) | 2025.02.26 |
| 백준: 17420. 깊콘이 넘쳐흘러 (C++) (0) | 2025.02.25 |


